IL ANALYTICS – is a plugin for computational library ILNumerics that introduces analytical capabilities to it. IL ANALYTICS provides integration between ILNumerics and ANALYTICS. The following extensions realized: Evaluation, Solution, Optimisation and Approximation. Evaluation assembly realizes total analytical calculation engine for ILNumerics arrays – double and complex. Solution assembly contains high-level classes to wrap nonlinear equation systems solution with ILNumerics solvers where the equations set up in analytical form. Optimisation assembly provides the same classes to solve optimization (unconstrained and constrained) problems set up via analytical expressions. Approximation assembly realizes linear and nonlinear least squares approximation of multivariable functions with arbitrary basis functions.

NOTE: ILAnalytics is free open source software, but for using it, you need to download and install the ILNumerics software (http://www.ilnumerics.net).

Download:

Source code: ILAnalytics.rar

Release binaries: ILAnalytics.Release.rar

ILNumerics page: http://ilnumerics.net/ilanalytics-a-plugin-for-ilnumerics.html

ILAnalytics Evaluation

Evaluation assembly contains realization of special Translator class – ILTranslator. This class registers analytical operations with ILNumerics double and complex arrays.  Registered operations include:
 - standard algebraic operators (+, -, *, /, ^);
 - special vector and matrix operators (dot product, transposition);
 - transcendental functions (sin, cos, exp, log and so on);
 - basic special functions (abs, sign, ceil and so on);
 - special functions (Bessel, gamma, error and so on);
 - linear algebra functions (LU decomposition, eigenvalues calculation and so on);
 - FFT operations.

ILAnalytics Solution

Solution assembly provides possibilities of solving nonlinear equation systems set up in analytical form with numerical solvers provided in ILNumerics.
Here is a code example for solving 3-variable equation system:

The result of solution presented below as text output and 3D visualization:

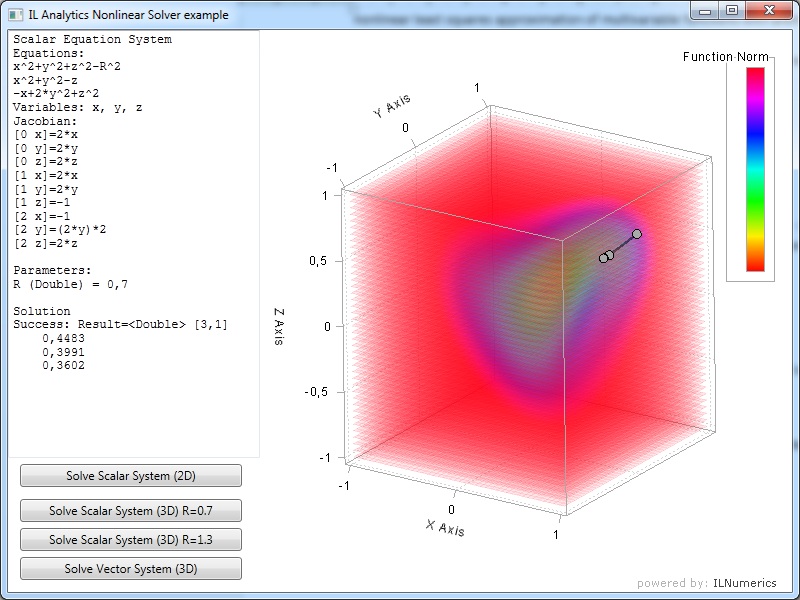
As can be seen from picture above, ILAnalytics provides analytical calculated Jacobian for nonlinear solver that can improve convergence process via more precise data calculation.  Also, the equation system is parametric – it contains ‘R’ parameter, that can be changed between solutions (without recreation of system data). So, the system can be sequentially solved for different parameter values.
Advantages of using analytical equation system solvers:
 - No need to write special classes for calculation delegates;
 - Easily storing data as strings (no need to make storage system for delegates);
 - More convenient data presentation for developer and user;
 - Automatically calculated derivatives for numerical solvers.
 - Parametrized system solution.

ILAnalytics Optimisation

Optimisation assembly provides possibilities of solving nonlinear optimization problems set up in analytical form with numerical solvers provided in ILNumerics. Solution result of an example constrained optimization problem presented below on the picture:

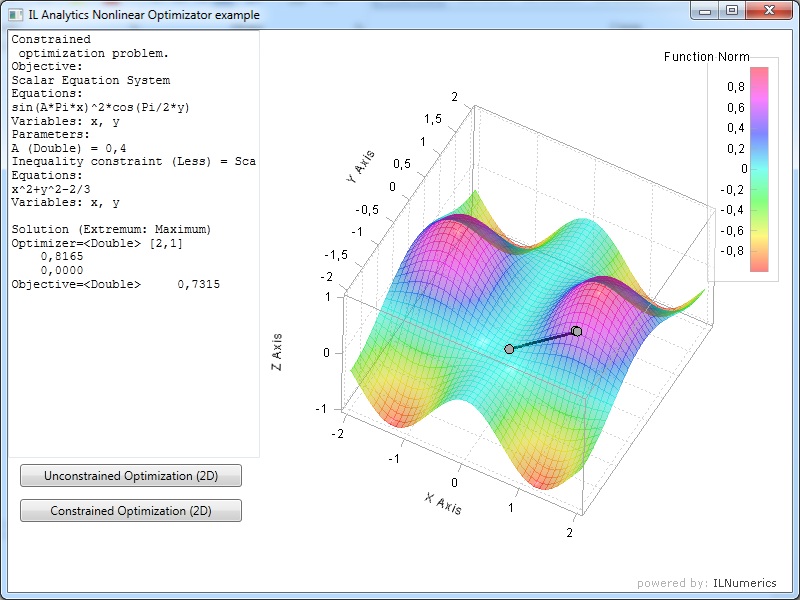
The objective function of the problem is equation system, presented in analytical form and depending on the parameter ‘A’. There is also constraint equation and extremum type is set up to ‘Maximum’.

The advantages of using analytical extension of optimization problems are the same as for nonlinear equation systems. Also, high level realization provides convenient constraint and extremum management: constraint type can be ‘Less’ or ‘More’ and extremum type – ‘Maximum’ or ‘Minimum’.

ILAnalytics Approximation

Approximation extension allows using ILNumerics approximation algorithms with arbitrary basis set up in the form of analytical expressions. Main functionality is:
- Linear least squares approximation.
- Nonlinear least squares approximation.
- Constructed linear and nonlinear multivariable bases of any order.
- Predefined linear and nonlinear 1D and 2D bases (exponential, polynomial, Fourier).

Two examples, linear and nonlinear approximation, presented below – code samples and result visualizations. Linear approximation:

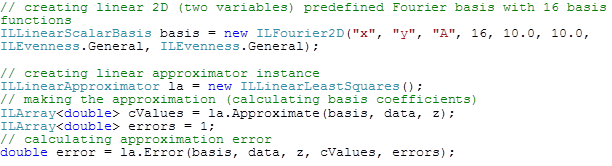
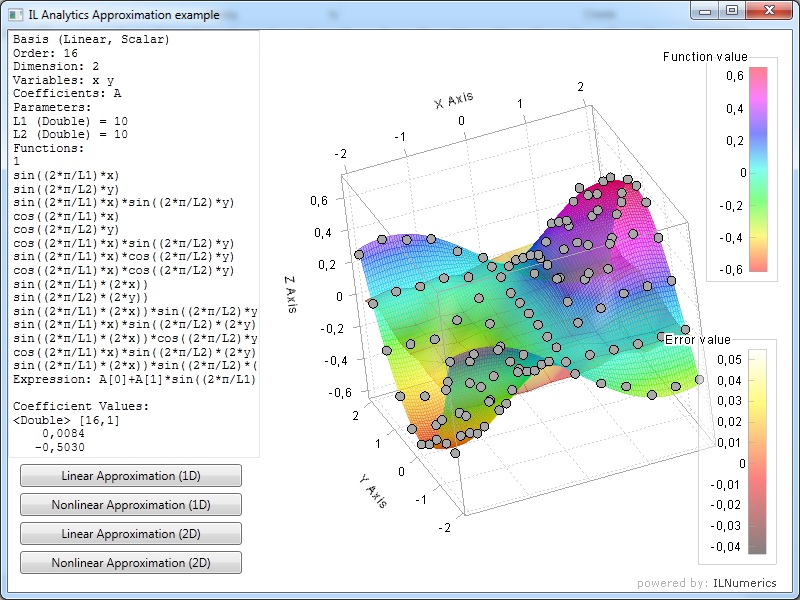
In the example of linear approximation, predefined 2D Fourier basis used for 2-variable function. Basis contains 16 function in total and is general in the sense of evenness – sin and cos functions used for both variables. Predefined parameters L1 and L2 are periods for the Fourier basis.

Nonlinear approximation:

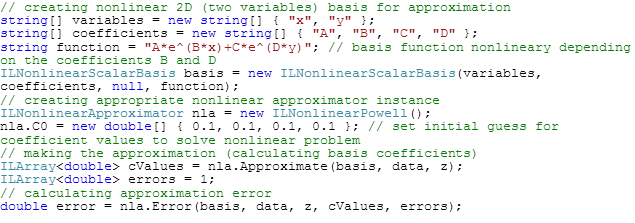
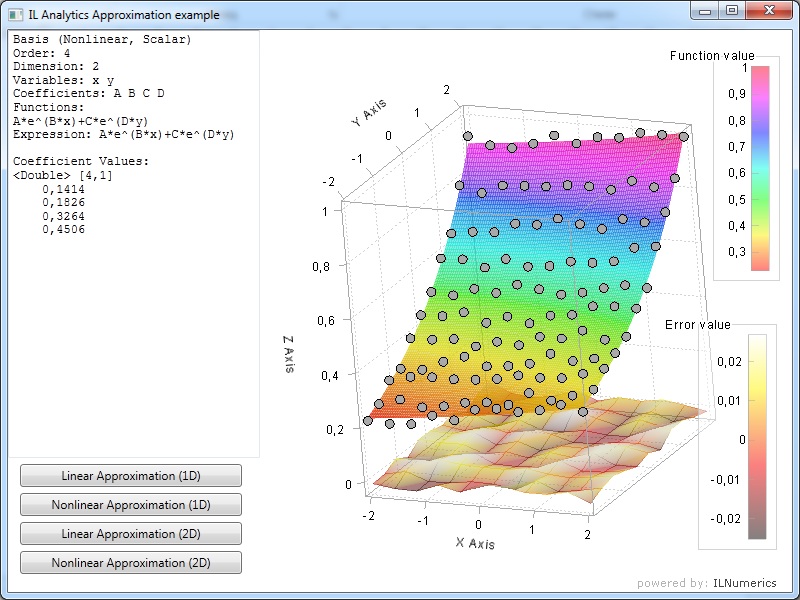
In the example of nonlinear approximation, new basis constructed from one expression. Basis is nonlinear and contains four coefficients A, B, C and D those found by created nonlinear approximator.

Both examples demonstrate the easiness of using analytical basis and approximators. Constructed bases and coefficients can be used subsequently for calculations and saved to files or transmitted over the network.

© Sergey L. Gladkiy